Therefore, what is Big-O notation? Big-O notation is used to describe a limit behavior of a function, or in other words, it is an upper-bound of a function. For two functions f(x) and g(x) which are subsets of real number, f(x) = O(g(x)) as x goes to infinity if and only if there is a positive real number M such that f (x) <= Mg(x) for all x. For example, f(x) = 4x^2 + 6x + 7 belongs to O(g(x)) where g(x) = 5x^2 for all x(real numbers).
Why studying the efficiency of sorting methods important especially the worst case? This is because in the real world, some insufficient sorting methods may take so long to compute which is meaningless. Hence, computing the efficiency of the program before applying it is very crucial.
Here is a table from Wikipedia about the Big-O notation of each sorting method:
| Name | Best | Average | Worst | Memory | Stable | Method | Other notes |
|---|---|---|---|---|---|---|---|
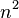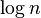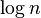| Quicksort |  | |  |  on average, worst case is  ; Sedgewick variation is worst case | typical in-place sort is not stable; stable versions exist | Partitioning | Quicksort is usually done in place with O(log n) stack space.[citation needed] Most implementations are unstable, as stable in-place partitioning is more complex. Naïve variants use an O(n) space array to store the partition.[citation needed] Quicksort variant using three-way (fat) partitioning takes O(n) comparisons when sorting an array of equal keys. |
| Merge sort | | | | worst case | Yes | Merging | Highly parallelizable (up to O(log n) using the Three Hungarian's Algorithm[clarification needed] or, more practically, Cole's parallel merge sort) for processing large amounts of data. |
| In-place merge sort | — | — |  |  | Yes | Merging | Can be implemented as a stable sort based on stable in-place merging.[2] |
| Heapsort | | | | | No | Selection | |
| Insertion sort | | 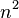| 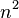| | Yes | Insertion | O(n + d),[clarification needed] where d is the number of inversions. |
| Introsort | | | | 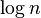| No | Partitioning & Selection | Used in several STL implementations. |
| Selection sort | 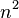| 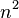| 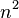| | No | Selection | Stable with O(n) extra space, for example using lists.[3] |
| Timsort | | | | | Yes | Insertion & Merging | Makes n comparisons when the data is already sorted or reverse sorted. |
| Shell sort | | or 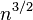 | Depends on gap sequence; best known is | | No | Insertion | Small code size, no use of call stack, reasonably fast, useful where memory is at a premium such as embedded and older mainframe applications. |
| Bubble sort | | 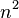| 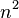| | Yes | Exchanging | Tiny code size. |
| Binary tree sort | | |  | | Yes | Insertion | When using a self-balancing binary search tree. |
| Cycle sort | — | 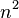| 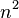| | No | Insertion | In-place with theoretically optimal number of writes. |
| Library sort | — | | 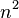| | Yes | Insertion | |
| Patience sorting | — | — | | | No | Insertion & Selection | Finds all the longest increasing subsequences in O(n log n). |
| Smoothsort | | | | | No | Selection | An adaptive sort: comparisons when the data is already sorted, and 0 swaps. |
| Strand sort | | 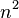| 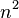| | Yes | Selection | |
| Tournament sort | — | | | [4] | ? | Selection | |
| Cocktail sort | | 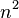| 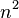| | Yes | Exchanging | |
| Comb sort | | | 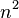| | No | Exchanging | Small code size. |
| Gnome sort | | 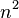| 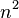| | Yes | Exchanging | Tiny code size. |
| UnShuffle Sort[5] |  | | | In place for linked lists. N*sizeof(link) for array. | Can be made stable by appending the input order to the key. | Distribution and Merge | No exchanges are performed. Performance is independent of data size. The constant 'k' is proportional to the entropy in the input. K = 1 for ordered or ordered by reversed input so runtime is equivalent to checking the order O(N). |
| Franceschini's method[6] | — | | | | Yes | ? | |
| Block sort[7] | | | | | Yes | Insertion & Merging | Combine a block-based O(n) in-place merge algorithm[8] with a bottom-up merge sort. Turns into a full-speed merge sort if additional memory is optionally provided to it. |
